Question

Find the points that are equidistant from both axes and the point (3 6)

Answer 1

Answer: (3,3) and (15,15)

==============================================

Step-by-step explanation:

The term "equidistant" means "equally distant".

We want (x,y) to be the same distance to the x axis, the y axis, and the point (3,6).

Let n represent this unknown equal distance. Negative distance doesn't make sense, so we'll have n > 0.

Start at the origin and move n units to the right to arrive at (n,0). We are n units from the y axis.

Now move n units up to arrive at (n,n). This point is guaranteed to be n units away from each axis.

That is one potential point. Other potential points are:

• (-n,n)
• (n,-n)
• (-n,-n)

One point for each quadrant.

Let's assume that the answer is in the 1st quadrant since (3,6) is located here.

We need to find an expression that represents the distance from the point (n,n) to (3,6). We'll set that distance expression equal to n so we can solve.

Part 1 of those steps

`d = √((x_1-x_2)^2+(y_1-y_2)^2)\\\\n = √((n-3)^2+(n-6)^2)\\\\n^2 = (n-3)^2+(n-6)^2\\\\n^2 = (n^2-6n+9)+(n^2-12n+36)\\\\n^2 = 2n^2-18n+45\\\\`

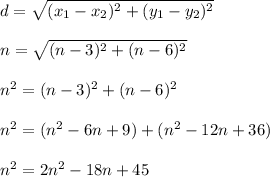
Part 2 of those steps

`0 = 2n^2-18n+45-n^2\\\\0 = n^2-18n+45\\\\n^2-18n+45 = 0\\\\(n-3)(n-15) = 0\\\\n-3 = 0\ \text{ or } \ n-15 = 0\\\\n = 3\ \text{ or } \ n = 15\\\\`

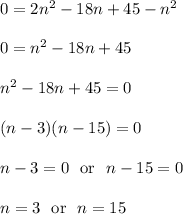
The quadratic formula could be used as an alternative pathway.

Therefore, the mystery point could be located at (3,3) or at (15,15)

Use the distance formula to verify each answer. I'll let you do this part.

---------

Extra info:

If you were to perform similar steps with the point (-n,n), then you'll find that no real numbered solutions exist. The two solutions would be complex numbers.

The cases (n,-n) and (-n,-n) have no solutions at all.

Therefore, we have confirmed only case (n,n) would work.