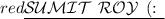Question

X² + y² +16y + 40 = 8x + 4y; center​

Answer 1

To find the center of the given equation, we need to rewrite it in the standard form of a circle equation, which is:

`\sf\:(x - h)^2 + (y - k)^2 = r^2 \\`

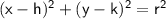
where (h, k) represents the center coordinates of the circle and r represents the radius.

Given equation:

`\sf\: x^2 + y^2 + 16y + 40 = 8x + 4y \\`

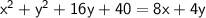
Rearranging the terms:

`\sf\:x^2 - 8x + y^2 + 16y - 4y = -40 \\`

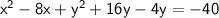
Completing the square for the x-terms:

`\sf\: (x^2 - 8x + 16) + y^2 + 12y - 4y = -40 + 16 \\`

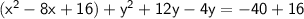
Completing the square for the y-terms:

`\sf\: (x^2 - 8x + 16) + (y^2 + 12y + 36) = -40 + 16 + 36 \\`

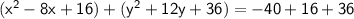
Simplifying:

`\sf\:(x - 4)^2 + (y + 6)^2 = 12 \\`

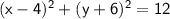
Comparing this with the standard form, we can see that the center of the circle is at (4, -6).

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`