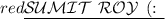Question

X² + y² + 2x-10y + 8 = 8y-46; radius​

Answer 1

To solve the equation and find the radius, we need to rewrite it in the form of a circle equation, which is (x - h)² + (y - k)² = r², where (h, k) represents the center of the circle and r represents the radius.

Given equation: x² + y² + 2x - 10y + 8 = 8y - 46

To rewrite the equation in the form (x - h)² + (y - k)² = r², we complete the square for both the x and y terms:

`\sf\:(x^2 + 2x) + (y^2 + 10y) = 8y - 46 - 8 \\`

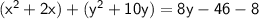
Completing the square for x terms:

`\sf\:x^2 + 2x = (x + 1)^2 - 1 \\`

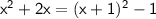
Completing the square for y terms:

`\sf\:y^2 + 10y = (y + 5)^2 - 25 \\`

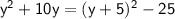
Substituting the completed square forms into the equation:

`\sf\:(x + 1)^2 - 1 + (y + 5)^2 - 25 + 8 = 8y - 46 - 8 \\`

Simplifying the equation:

`\sf\:(x + 1)^2 + (y + 5)^2 = 8y - 46 - 8 + 1 + 25 - 8 \\`

`\sf\:(x + 1)^2 + (y + 5)^2 = 8y - 36 \\`

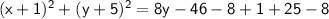
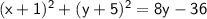
Now we can see that the equation is in the form of (x - h)² + (y - k)² = r², where h = -1, k = -5, and r² = 8y - 36. Therefore, the radius is
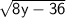`\sf\:√(8y - 36) \\`.

`\huge{\mathfrak{\colorbox{black}{\textcolor{lime}{I\:hope\:this\:helps\:!\:\:}}}}`

♥️
`\large{\textcolor{red}{\underline{\mathcal{SUMIT\:\:ROY\:\:(:\:\:}}}}`