Question

Arun is going to invest $7,700 and leave it in an account for 20 years. Assuming the interest is compounded continuously, what interest rate, to the nearest hundredth of a percent, would be required in order for Arun to end up with $13,100?

Answer 1

The rate required is approximately 2.66%.

Explanation:

Formula:
`A = Pe^(rt)`

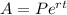
where A is the value is the final amount at the end of the period

P is the principal

e is the mathematical constant 2.71828

r is the rate

t is the time in years

Given:

P = $7,700

t = 20 years

A = $13,100

Asked: interest rate r

Substitute the values and then solve

`A = Pe^(rt)`

`13,100 = 7,700(e)^(r(20))\\13,100 = 7,700(e)^(20r)\\13,100/7,700 = e^(20r)\\(131)/(77) = e^(20r)\\ln ((131)/(77) = e^(20r))\\ln((131)/(77) = ln(e^(20r))\\ln ((131)/(77) ) = 20r\\r = (ln((131)/(77)) )/(20) \\r = 0.0265696\\`

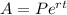
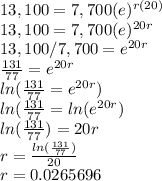
Multiply it by 100% to change the decimal value to percent and take the value up to the hundredths place

r = 0.0265696 * 100%

r = 2.66%