Question

10- A block attached to a spring oscillates in simple harmonic motion along the x axis. The

limits of its motion are x = 10cm and x = 50 cm and it goes from one of these extremes to
the other in 0.25 s. Its amplitude and frequency are:
A 40 cm. 2Hz
B. 20 cm, 4Hz
C. 40cm, 2Hz
D. 25 cm, 4Hz
E. 20 cm, 2Hz

Answer 1

Choice E.

Amplitude:
`20\; {\rm cm}`.

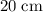Frequency:
`2\; {\rm Hz}`.

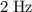Step-by-step explanation:

The amplitude of a simple harmonic motion (SHM) is the maximum displacement from equilibrium.

In this question, the equilibrium is in the center of the two extremes. With one extreme at
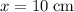`x = 10\; {\rm cm}` and the other at
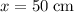`x = 50\; {\rm cm}`, the center will be at
`(1/2)\, (10 + 50)\; {\rm cm} = 30\; {\rm cm}`.

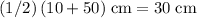The maximum displacement will be
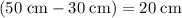`(50\; {\rm cm} - 30\; {\rm cm}) = 20\; {\rm cm}` (or equivalently,
`(30\; {\rm cm} - 10\; {\rm cm}) = 20\; {\rm cm}`.

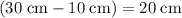Frequency measures the number of cycles completed in unit time (e.g., one second.) In one full cycle of an SHM, the oscillator will travel from one extreme to another and then back to the original extreme. In this question:

• Travel from one extreme to the other:
  `0.25\; {\rm s}`.
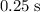• Travel from the other extreme back to the original one:
  `0.25\; {\rm s}`.

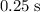In other words, one full cycle of this SHM will take
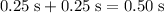`0.25\; {\rm s} + 0.25\; {\rm s} = 0.50\; {\rm s}`. The period of this SHM will be
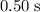`0.50\; {\rm s}`. Hence, the frequency of this SHM will be:

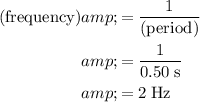`\begin{aligned} (\text{frequency}) &= \frac{1}{(\text{period})} \\ &= \frac{1}{0.50\; {\rm s}} \\ &= 2\; {\rm Hz}\end{aligned}`.