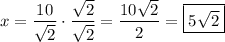Solve for the indicated unknown part of each triangle

Question

asked Oct 1, 2024 165k views

1 Answer

Sorabzone · Answer 1 · 2024-10-05T18:06:43+0000

Answer and Explanation:

1) We can solve for the measure of
$\theta$ in this triangle by using the trigonometric ratio tangent.

$\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}$

↓ plugging in the given side values

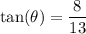
$\tan(\theta) = (8)/(13)$

↓ taking the inverse tangent of both sides

$\boxed{\theta = \tan^(-1)\left((8)/(13)\right)}$

2) We can solve for the measure of
$\theta$ in this triangle by (once again) using the trigonometric ratio tangent.

$\tan(\theta) = \frac{\text{opposite}}{\text{adjacent}}$

↓ plugging in the given side values

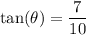
$\tan(\theta) = (7)/(10)$

↓ taking the inverse tangent of both sides

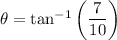
$\theta = \tan^(-1)\left((7)/(10)\right)$

3) We can solve for the length of side x by using the ratio of the sides of a 45-45-90 triangle, which is:

So, to solve for x, we just have to divide the length of the hypotenuse by
$\sqrt2$ :

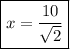
$\boxed{x = (10)/(√(2))}$

Note that this can be rationalized by multiplying the fraction by
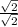$(\sqrt2)/(√(2))$ :

$x = (10)/(√(2)) \cdot (\sqrt2)/(\sqrt2) = (10\sqrt2)/(2) = \boxed{5\sqrt2}$