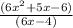Question

The area of a rectangle is 6x^2 + 5x – 6, and its width is 3x – 2. What is the length of the rectangle? if the width is doubled what is the length?

Answer 1

`((6x^2 + 5x - 6))/((6x - 4))`

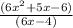
Explanation:

To find the length of the rectangle, we need to divide the area by the width, since Area = Length × Width. Let's solve the problem step by step:

Given:

Area of the rectangle =
`6x^2 + 5x - 6`

Width of the rectangle =
`3x - 2`

We'll divide the area by the width to find the length:

Length = Area / Width

Length =
`((6x^2 + 5x - 6))/( (3x - 2))`

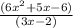
To find the length when the width is doubled, we'll multiply the original width by 2:

New Width =
`2 * (3x - 2) = 6x - 4`

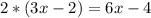
New Length = Area / New Width

Now, let's solve for the length in both cases:

Length of the rectangle:

Length =
`((6x^2 + 5x - 6))/( (3x - 2))`

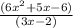
Length of the rectangle when the width is doubled:

New Length =
`((6x^2 + 5x - 6))/((6x - 4))`