Question

Is the product of √1024 and -3.4 rational or irrational? Explain your answer.

Answer 1

Rational as it is a terminating decimal.

Explanation:

Given expression:

`√(1024) \cdot -3.4`

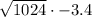
Rewrite 1024 as 32²:

`\implies √(32^2) \cdot -3.4`

`\textsf{Apply radical rule} \quad √(a^2)=a, \quad a \geq 0`

`\implies 32 \cdot -3.4`

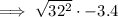
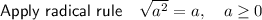
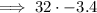
Multiply the numbers:

`\implies -108.8`

Therefore, the product is a terminating decimal.

A rational number is a number that can be expressed as the ratio of two integers (where the denominator does not equal zero).

A terminating decimal can be written as a rational number.

To convert a terminating decimal into a rational number, multiply the number by a multiple of 10 that eliminates the decimal, then divide by the same number:

`\implies (-108.8 \cdot 10)/(10)`

`\implies -(1088)/(10)`

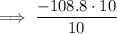
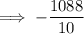
Reduce the fraction to its simplest form by dividing the numerator and denominator by 2:

`\implies -(544)/(5)`

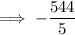
Therefore, the product of √1024 and -3.4 is rational as it is a terminating decimal.

Answer 2

• The product is rational

-------------------------------------------

The first number is:

• 
  `√(1024) =√(32^2) =32`

And the second number is -3.4.

Both numbers are rational, hence their product is rational.