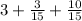A common denominator is a shared multiple of the denominators of the fractions involved when adding or subtracting fractions. It enables fraction comparison and addition/subtraction.
Simplification is the process of reducing a fraction to its simplest form by dividing the numerator and denominator by their greatest common divisor. This is done to represent fractions in the simplest terms viable.
Conversion: The process of transferring a fraction from one form to another while retaining its equal value is known as conversion. Finding a common denominator or expressing a fraction in terms of a specified unit or fraction may be required.
Fraction Addition/Subtraction: When adding or subtracting fractions, a common denominator is required. This entails determining a common multiple of
To rewrite the expression 3 + 1/5 + 2/3 using fifteenths as the common denominator, we need to find a common denominator for 5 and 3, which is 15 (since 5 and 3 are both factors of 15).
First, let's convert the fractions 1/5 and 2/3 to fifteenths:
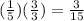
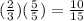
Now we can rewrite the expression using the common denominator: