The property used to rewrite
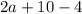 as
as
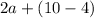 is the associative property. Therefore, option 2 is correct
is the associative property. Therefore, option 2 is correct
The image shows a sequence of steps simplifying an algebraic expression, and each step is labeled with the property of arithmetic that justifies the transition from one step to the next.
The first step applies the distributive property to expand
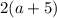 into
into
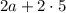 . The distributive property allows you to multiply a single term by each term inside a set of parentheses.
. The distributive property allows you to multiply a single term by each term inside a set of parentheses.
The expression goes from:
![\[ 2(a + 5) - 4 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fywxg5xunawao1me0s90a3njfclkqstky9.png)
to:
![\[ 2 \cdot a + 2 \cdot 5 - 4 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4cazk4y1tevbbr820uin1g7fp0mt746ver.png)
which simplifies to:
![\[ 2a + 10 - 4 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/676zylc7mdnrie54o3qvekebutwlu7ezwz.png)
The next step shown in the image is where the
 inside the parentheses is combined into
inside the parentheses is combined into
 . This step uses the associative property of addition, which states that the way in which terms are grouped does not change their sum.
. This step uses the associative property of addition, which states that the way in which terms are grouped does not change their sum.
So the full sequence represented in the image is an application of the distributive property followed by an application of the associative property. The final step groups the constant terms together and combines them, which is also an application of the associative property.
Thus, the property used to rewrite
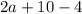 as
as
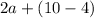 is the associative property.
is the associative property.