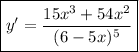Question

Differentiate the following function. y = 3x³ / (6-5x)⁴. dy/dx =

Answer 1

`y' = (15x^3 + 54x^2)/((6-5x)^5)`

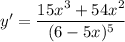
Explanation:

Given the function:

`y= (3x^3)/((6-5x)^4)`

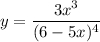
We can find the equation of its derivative using the quotient rule:

`\left((f(x))/(g(x))\right)' = (g(x) \cdot f'(x) - f(x) \cdot g'(x))/((g(x))^2)`

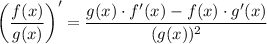
First, we should find the derivative of the function's numerator [which I will label
`f(x)` ] and its denominator [which I will label
`g(x)` ].

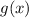Numerator

`f(x) = 3x^3`

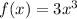
↓ applying the power rule ...
`(x^a)' = ax^(a - 1)`

`f'(x) = 3 \cdot 3x^(3-1)`

`f'(x) = 9x^2`

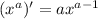
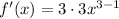
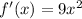
Denominator

`g(x) = (6-5x)^4`

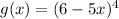
↓ applying the chain rule ...
`\left[\frac{}{}f(x)^n\frac{}{}\right]' = n\left[\frac{}{}f(x)\frac{}{}\right]^(n-1) \cdot f'(x)`

`g'(x) = -20(6-5x)^3`

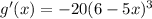
Next, we can plug these functions into the quotient rule.

`y' = \frac{(6-5x)^4 \left[\frac{}{} 9x^2 \frac{}{}\right] - 3x^3 \left[ \, -20(6-5x)^3\frac{}{}\right]}{((6-5x)^4)^2}`

↓ simplifying the exponent on the bottom ...
`(x^a)^b = x^(a\,\cdot \,b)`

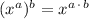
`y' = \frac{(6-5x)^4 \left[\frac{}{} 9x^2 \frac{}{}\right] - 3x^3 \left[ \, -20(6-5x)^3\frac{}{}\right]}{(6-5x)^8}`

↓ factoring
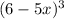`(6-5x)^3` out of the numerator

`y' = \frac{(6-5x)^3 \left(\frac{}{} 9x^2(6-5x) + 60x^3 \frac{}{}\right)}{(6-5x)^8}`

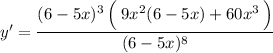
↓ canceling
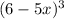`(6-5x)^3` with the denominator

`y' = \frac{\left(\frac{}{} 9x^2(6-5x) + 60x^3 \frac{}{}\right)}{(6-5x)^(8\,-\,3)}`

`y' = (9x^2(6-5x) + 60x^3)/((6-5x)^5)`

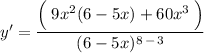
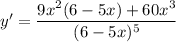
↓ applying the distributive property to
`9x^2(6-5x)` ...
`A(B+C) = AB + AC`

`y' = ((54x^2-45x^3) + 60x^3)/((6-5x)^5)`

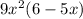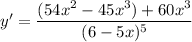
↓ combining like terms in the numerator

`\boxed{y' = (15x^3 + 54x^2)/((6-5x)^5)}`

Answer 2

`\displaystyle (dy)/(dx)=(15x^3+54x^2)/((6-5x)^5)`

Explanation:

`\displaystyle y=(3x^3)/((6-5x)^4)\\\\(dy)/(dx)=((6-5x)^4(3x^3)'-(3x^3)((6-5x)^4)')/(((6-5x)^4)^2)\\\\(dy)/(dx)=(9x^2(6-5x)^4-(3x^3)(-20(6-5x)^3))/((6-5x)^8)\\\\(dy)/(dx)=(9x^2(6-5x)^4+60x^3(6-5x)^3)/((6-5x)^8)\\\\(dy)/(dx)=(9x^2(6-5x)+60x^3)/((6-5x)^5)\\\\(dy)/(dx)=(54x^2-45x^3+60x^3)/((6-5x)^5)\\\\(dy)/(dx)=(15x^3+54x^2)/((6-5x)^5)`

Make sure to use quotient rule!