Length of Simon's tent = 6 feet
Distance from the bottom of the tent to the tent's base = 8 feet
Let the length of rope be R.
The tent and the rope forms a right angle triangle where the rope is the hypotenuse.
We know that :
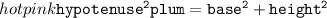
Which means :
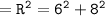
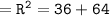
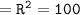
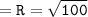
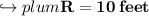
Thus, the hypotenuse of this triangle = 10 feet
▪︎Therefore, the length of the rope = 10 feet