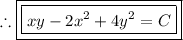Question

Find the general solution of the following differential equation. Primes denote derivatives with respect to x. (x+8y)y' = 4x-y The general solution is (Type an implicit general solution in the form F(x,y) = C, where C is an arbitrary constant. Type an expression using x and y as the variables.)

Previous question

Answer 1

`xy-2x^2+4y^2=C`

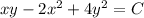
Explanation:

Solve the given differential equation.

`(x+8y)(dy)/(dx) = 4x-y`

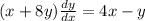
(1) - Rearrange the differential equation

`(x+8y)(dy)/(dx) = 4x-y\\\\\Longrightarrow (x+8y)dy=(4x-y)dx\\\\\Longrightarrow -(4x-y)dx+ (x+8y)dy\\\\\Longrightarrow \boxed{ (-4x+y)dx+ (x+8y)dy}`

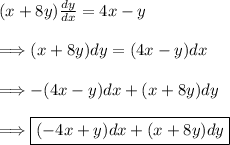
(2) - Check to see if this is an exact differential equation

`M=-4x+y \ and \ N=x+8y \ \text{the DE is exact if} \ M_y=N_x\\\\\left\begin{array}{ccc}M_y=1\\N_x=1\end{array}\right\} \ M_y=N_x \therefore \ Exact`

(3) - Integrate M with respect to x and N with respect to y

`\int(-4x+y)dx\\\\\Longrightarrow \boxed{ -2x^2+xy}\\\\\int(x+8y)dy\\\\\Longrightarrow \boxed{xy+4y^2}`

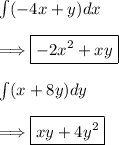
(4) Form the solution. The solution will be the two evaluated integrals from above added together ignoring any duplicate terms

`\therefore \boxed{\boxed{xy-2x^2+4y^2=C}}`