Question

Find the sum of the first one hundred terms in the progression. (-6, -2, 2...) (Rigorous) A. B. C. D. 19,200 19,400 -604 604

Answer 1

Answer: 19,200

Explanation:

The nth term of an arithmetic progression can be found by the formula:

`a_(n) = a_(1) + (n-1) * d`

Where:

`a_(n)` = nth term

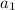`a_(1)` = first term = -6

n = number of terms = 100

d = common difference = 4

The 100th term (
`a_(100)`) would therefore be:

`a_(100)` = -6 + (100-1) * 4 = -6 + 99 * 4 = 390

The sum
`S_(n)` of the first n terms of an arithmetic sequence can be found using the formula:

`S_(n) = (n)/(2) *(a_(1) + a_(n) )`

So the sum of the first 100 terms (
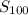`S_(100)`) would be:

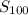`S_(100)` = 100/2 * (-6 + 390) = 50 * 384 = 19200

So, the sum of the first 100 terms of the given arithmetic progression is 19200

Answer 2

19,200

Explanation:

d = (-2) - (-6) = 4

a_1 = -6

S_n = (n/2)[2a_1 + (n - 1)d]

S_100 = (100/2)[2 × (-6) + (100 - 1)(4)]

S_100 = 50(-12 + 99(4)]

S_100 = 50(384)

S_100 = 19,200