Question

y varies jointly as x and the square of z and inversely as n. if y=80 when x=9, z=4, and n=18, find y when x=32, z=7, and n=35

Answer 1

`y=448`

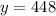
Explanation:

To solve this problem, we'll use the concept of joint variation and inverse variation.

Given that y varies jointly as x and the square of z and inversely as n. We can express this mathematically as...

`y \propto (xz^2)/(n)`

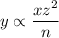
Add a direct Proportion constant, "k," to get rid of the proportion sign.

`y \propto (xz^2)/(n)\\\\\Longrightarrow y =k(xz^2)/(n)`

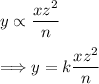
Now using the fact that y=80 when x=9, z=4, and n=18. We can find the value of "k."

`y =k(xz^2)/(n)\\\\\Longrightarrow 80=k((9)(4)^2)/(18) \\\\\Longrightarrow 80=k((9)(16))/(18) \\\\\Longrightarrow 80=k(144)/(18) \\\\\Longrightarrow 80=8k\\\\\Longrightarrrow \boxed{k=8}`

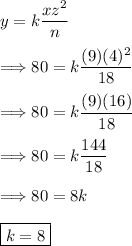
Thus, we have...

`y =(10xz^2)/(n)`

Now we can plug in x=37,z=7, and n=35 to find y.

`y =(8xz^2)/(n)\\\\\Longrightarrow y =(10(32)(7)^2)/(35)\\\\\Longrightarrow y =(10(32)(49))/(35)\\\\\Longrightarrow y =(15680)/(35)\\\\\therefore \boxed{\boxed{y=448}}`