Question

2tan(x/2)- csc x=0 interval [0,2pi)

Answer 1

`x= (\pi)/(3), \;\;x=(5 \pi)/(3)`

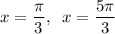
Explanation:

Given trigonometric equation:

`2 \tan\left((x)/(2)\right)- \csc x=0`

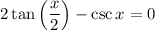
To solve the equation for x in the given interval [0, 2π), first rewrite the equation in terms of sin x and cos x using the following trigonometric identities:

`\boxed{\begin{minipage}{4cm}\underline{Trigonometric identities}\\\\$\tan \left((\theta)/(2)\right)=(1-\cos \theta)/(\sin \theta)$\\\\\\$\csc \theta = (1)/(\sin \theta)$\\ \end{minipage}}`

Therefore:

`2 \tan\left((x)/(2)\right)- \csc x=0`

`\implies 2 \left((1-\cos x)/(\sin x)\right)- (1)/(\sin x)=0`

`\implies (2(1-\cos x))/(\sin x)- (1)/(\sin x)=0`

`\textsf{Apply the fraction rule:\;\;$(a)/(c)-(b)/(c)=(a-b)/(c)$}`

`(2(1-\cos x)-1)/(\sin x)=0`

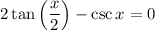
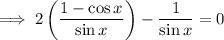
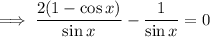
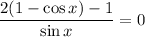
Simplify the numerator:

`(1-2\cos x)/(\sin x)=0`

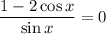
Multiply both sides of the equation by sin x:

`1-2 \cos x=0`

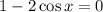
Add 2 cos x to both sides of the equation:

`1=2\cos x`

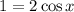
Divide both sides of the equation by 2:

`\cos x=(1)/(2)`

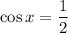
Now solve for x.

From inspection of the attached unit circle, we can see that the values of x for which cos x = 1/2 are π/3 and 5π/3. As the cosine function is a periodic function with a period of 2π:

`x=(\pi)/(3) +2n\pi,\; x=(5\pi)/(3) +2n\pi \qquad \textsf{(where $n$ is an integer)}`

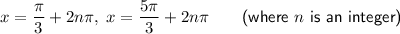
Therefore, the values of x in the given interval [0, 2π), are:

`\boxed{x= (\pi)/(3), \;\;x=(5 \pi)/(3)}`