Question

Suppose that there are 14 songs on a new album and you like 8 of them. If you play the album with shuffle (i.e. it randomly selects the order of the songs and plays them once), what is the probability that among the first two songs (a) You like both of them (b) You like neither of them (c) You like exactly one of them

Answer 1

(a) You like both of them,

Total Probability = 4/13 = 0.308

(b) You like neither of them,

Total Probability = 15/91 = 0.165

(c) You like exactly one of them,

Total Probability = 24/91 = 0.264

Explanation:

Total number of songs = T = 14

Songs that you like = S = 8

so, if you pick a random song, the probability that it's one you like is,

P = 8/14= 4/7

and that you don't like it is, 1- 4/7 = 3/7 = Q

Now, we look at the cases,

(a) Among the first two, you like both of them,

The probability the we like the first is P = 4/7 (calculated above)

Now, after we have picked/played one of the songs, there are 13 songs left in the album and 7 of those we like (since we just listened to one of the ones which we liked)

so the probability that the second song is also going to be one which we like is,

P2 = (7/13)

The total probability of liking both is the product of these two so,

`Probability \ for \ liking \ both =(4/7)(7/13) = 4/13`

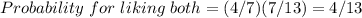
(b) You like neither of them,

In this case, the probability of not liking the first one is Q = 3/7

Then there will be 13 songs left out of which we like 8, which means that we don't like 13-8 = 5

and the probability of the 2nd song being one which we don't like will be,

Q2 = 5/13

and for the total probability, we get,

`Probability \ for \ liking \ neither =(3/7)(5/13) = 15/91`

(c) You like exactly one of them,

In this case, if we like the first one, then P = 4/7 but then the probability of liking the 2nd one also is(calculated in (a)) P2 = 7/13 but in this case, we like only one so we have to find the probability of not liking the 2nd one which is, 1-7/13 = 6/13

so the total probability of liking only one will be,

`Probability \ for \ liking \ only \ one =(4/7)(6/13) = 24/91`

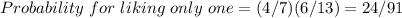
The total probability will not change if we don't like the first one and like the 2nd one,

in that case,

`Probability \ for \ liking \ only \ one =(3/7)(8/13) = 24/91`

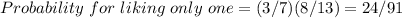
so we get same answer either way

Answer 2

I think the answer might be either a or c