Question

The rates of on-time flights for commercial jets are continuously tracked by the U.S. Department of Transportation. Recently, Southwest Air had the best rate with 80 % of its flights arriving on time. A test is conducted by randomly selecting 16 Southwest flights and observing whether they arrive on time. (a) Find the probability that exactly 8 flights arrive on time.

Answer 1

The probability that exactly 8 arrive on time is,

p(x=8) = 0.553%

Explanation:

Since 80% of the flights arrive on time, that is a probability of 0.8 = P

Now, if we randomly select 16 flights, 80% of them will arrive on time,

So, this is the Binomial Distribution,

Which has the formula,

`p(x) = (n!/x!(n-x)!)(P^x)(Q^(n-x) )`

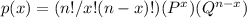
here, x is the number of successes, in our case, x = 8 (since 8 arrive on time)

P = probability of success = 0.8

Q = probability of failure = 1- P = 0.2

i.e. 20% don't arrive on time

n is the number of trials, in our case, n = 16

since 16 flights are selected

then, the probability for 8 coming on time is,

`p(8) = (16!/8!(16-8)!)(0.8^8)(0.2^(16-8) )`

for the first part,

`(16!/8!(16-8)!)\\16!/8!8!\\= 12870`

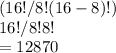
now,

`0.8^8=0.1678`

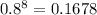
and

`0.2^8=2.56*10^(-6)`

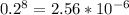
multiplying all these together to get the answer,

`(12870)(0.1678)(2.56*10^(-6))`

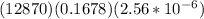
which gives,

`p(x=8)= 5.5285*10^(-3)`

or,

`p(x=8) = 0.00553`

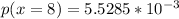
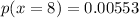
or, p(x=8) = 0.553%