Question

A map of the town that Annie and Barbara live in can be represented by the Cartesian plane. Annie is located at $(5,-11)$ and Barbara says she is located at $(-7,13)$. They agree to meet at the midpoint of the segment formed by their current locations. However, it turns out that Barbara read the map wrong, and Barbara is actually at $(-5,5)$. What is the positive difference in the $y$-coordinates of where they agreed to meet and where they should actually meet

Answer 1

The positive difference in the 'y' coordinates of where they agreed to meet and where they should actually meet is 4

Explanation:

The segement they form is, using the distance formula,

`d=√(((x1-x2)^2+(y1-y2)^2))`

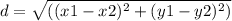
but since we only need to find the y coordinates,

we do not need it in this case

now ,

in our case, x1 = 5, y1 = -11

x2=-7, y2=13

so,

y1-y2 is the total y difference for the first points,

so d1=-11-13

d1 = -24

but since distance is positive,so,

d1 = 24

and the midpoint of that would be m= d/2,

m1 = 12

if Barbara is at (-5,5), then the distance will be,

since then, x2=-5,y2=5,

d2 = -11-5

d2=-16

or,

d2 = 16

and

m2 = 16/2

m2 = 8

so the positive difference in the 'y' coordinates of where they agreed to meet and where they should actually meet is,

diff = 12-8

diff = 4

so the difference in y coordinates is 4