Question

Right triangle EFG has its right angle at F, EG = 6 , and FG = 4 What is the value of the trigonometric ratio of an angle of the triangle? Drag a value to each box to match the trigonometric ratio with its value .​

Answer 1

`\cos G=(2)/(3)`

`\csc E=(3)/(2)`

`\cot G=(2)/(√(5))`

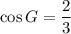
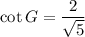
Explanation:

If the right angle of right triangle EFG is ∠F, then EG is the hypotenuse, and EF and FG are the legs of the triangle. (Refer to attached diagram).

Given ΔEFG is a right triangle, and EG = 6 and FG = 4, we can use Pythagoras Theorem to calculate the length of EF.

`\begin{aligned}EF^2+FG^2&=EG^2\\EF^2+4^2&=6^2\\EF^2+16&=36\\EF^2&=20\\√(EF^2)&=√(20)\\EF&=2√(5)\end{aligned}`

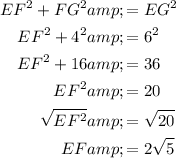
Therefore:

• EF = 2√5
• FG = 4
• EG = 6

`\hrulefill`

To find cos G, use the cosine trigonometric ratio:

`\boxed{\begin{minipage}{9 cm}\underline{Cosine trigonometric ratio} \\\\$\sf \cos(\theta)=(A)/(H)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

For angle G, the adjacent side is FG and the hypotenuse is EG.

Therefore:

`\cos G=(FG)/(EG)=(4)/(6)=(2)/(3)`

`\hrulefill`

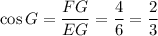
To find csc E, use the cosecant trigonometric ratio:

`\boxed{\begin{minipage}{9 cm}\underline{Cosecant trigonometric ratio} \\\\$\sf \csc(\theta)=(H)/(O)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

For angle E, the hypotenuse is EG and the opposite side is FG.

Therefore:

`\csc E=(EG)/(FG)=(6)/(4)=(3)/(2)`

`\hrulefill`

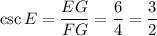
To find cot G, use the cotangent trigonometric ratio:

`\boxed{\begin{minipage}{9 cm}\underline{Cotangent trigonometric ratio} \\\\$\sf \cot(\theta)=(A)/(O)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

For angle G, the adjacent side is FG and the opposite side is EF.

Therefore:

`\cot G=(FG)/(EF)=(4)/(2√(5))=(2)/(√(5))`