Answer:
24 cm²
Explanation:
The area of a rhombus is half the product of its diagonals.
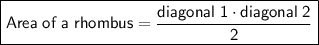
Therefore, to find the area of the rhombus, we need to find the lengths of the diagonals AC and BD.
The diagonals of a rhombus are perpendicular bisectors of each other.
The point of intersection of the diagonals of rhombus ABCD is point O.
We can use the given information to find the lengths of BO and OC, then double these to find diagonals AC and BD.
The sides of a rhombus are equal in length. Therefore, if the perimeter of rhombus ABCD is 20 cm, each side length is 5 cm.
Therefore, the hypotenuse of right triangle BOC is BC = 5 cm.
If the ratio of AC : BD = 4 : 3, then the ratio of OC : BO = 2 : 1.5.
Let OC = 2x and BO = 1.5x.
Use Pythagoras Theorem to find the value of x.
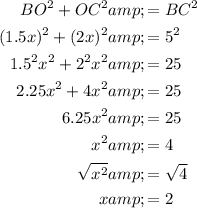
Therefore, to find the lengths of OC and BO, substitute x = 2:
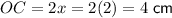
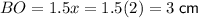
As the diagonals of a rhombus bisect each other:

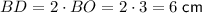
Finally, substitute the lengths of the diagonals into the formula for the area of a rhombus:

Therefore, the area of rhombus ABCD is 24 cm².