Question

Please help!!!!!!!!!!!!!!!!!!!!!!!!

Answer 1

18 cm²

Explanation:

The area of a right triangle is half the product of its base and height.

`\boxed{A=(1)/(2)bh}`

Given the right angle of triangle ABC is angle C, this means that AB is its hypotenuse.

The side opposite angle A is BC, the base of the right triangle.

The side adjacent angle A is AC, the height of the right triangle.

To calculate the lengths of the sides BC and AC, we can use the sine and cosine trigonometric ratios.

`\boxed{\begin{minipage}{9.4 cm}\underline{Trigonometric ratios} \\\\$\sf \sin(\theta)=(O)/(H)\quad\cos(\theta)=(A)/(H)\quad\tan(\theta)=(O)/(A)$\\\\where:\\ \phantom{ww}$\bullet$ $\theta$ is the angle. \\ \phantom{ww}$\bullet$ $\sf O$ is the side opposite the angle. \\\phantom{ww}$\bullet$ $\sf A$ is the side adjacent the angle. \\\phantom{ww}$\bullet$ $\sf H$ is the hypotenuse (the side opposite the right angle). \\\end{minipage}}`

Given values:

• θ = ∠A = 75°
• O = BC = b
• A = AC = h
• H = AB = 12

Substitute these values into the sine and cosine ratios to create expressions for the base (b) and height (h) of the right triangle ABC.

`\boxed{\begin{aligned}\sin A&=(BC)/(AB)\\\\\sin 75^(\circ)&=(b)/(12)\\\\b&=12\sin 75^(\circ)\end{aligned}}`
`\boxed{\begin{aligned}\cos A&=(AC)/(AB)\\\\\cos 75^(\circ)&=(h)/(12)\\\\h&=12\cos75^(\circ)\end{aligned}}`

To calculate the area of triangle ABC, substitute the found expressions for b and h into the area of a triangle formula.

`\begin{aligned}\textsf{Area of $\triangle ABC$}&=(1)/(2)bh\\\\&=(1)/(2) \cdot 12 \sin 75^(\circ) \cdot 12 \cos 75^(\circ)\\\\&=72\sin 75^(\circ) \cos 75^(\circ)\\\\&=72 \cdot (\sin 150^(\circ))/(2)\\\\& = 36\sin 150^(\circ)\\\\& = 36 \cdot (1)/(2)\\\\&=18\; \sf cm^2\end{aligned}`

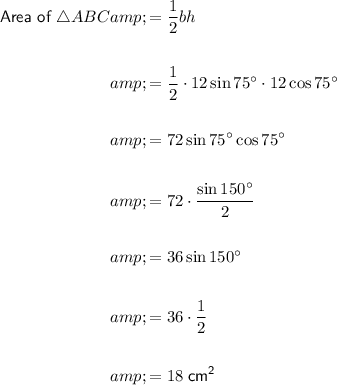
Therefore, the area of triangle ABC is 18 square centimeters.