Question

A diameter of a circle has endpoints P(-7, 2) and Q(3, -8).

a. Find the center of the circle.
b. Find the radius. If your answer is not an. integer, express it in radical form.
c. Write an equation for the circle.

Answer 1

centre: (-2, -3).

radius :
`5 √(2)`

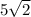
equation:
`x^2 + 4x + y^2 + 6y - 31 = 0`

Explanation:

a. Find the center of the circle:

The center of a circle is the midpoint of its diameter.

So, the center of the circle with endpoints P(-7, 2) and Q(3, -8) is the midpoint of the line segment connecting those points.

The midpoint of a line segment with endpoints (x1, y1) and (x2, y2) is given by the formula:

Sure, here are the answers to your questions:

`((x_1+x_2)/(2),(y_1+y_2)/(2))`

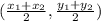
In this case, the midpoint of the line segment connecting P(-7, 2) and Q(3, -8) is:

`((-7 + 3)/(2), (2 - 8)/(2))=( -2, -3)`

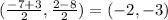
Therefore, the center of the circle is (-2, -3).

b. Find the radius.

The radius of a circle is the distance from the center of the circle to any point on the circle.

In this case, we can find the radius by finding the distance between the center of the circle (-2, -3) and any one of the endpoints of the diameter. Let's use the endpoint P(-7, 2). The distance formula tells us that the distance between two points is given by the formula:

`√((x_1 - x_2)^2 + (y_1 - y_2)^2)`

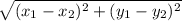
In this case, the distance between the center of the circle (-2, -3) and the endpoint P(-7, 2) is:

`√((-2 - (-7))^2 + ((-3) - 2)^2) \\ = √(25 + 25) \\ = √(50) \\ = 5\sqrt2`

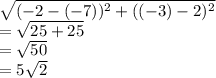
Therefore, the radius of the circle is
`5 √(2)`

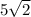
c. Write an equation for the circle.

The equation of a circle with center (a, b) and radius r is given by the formula:

`(x - a)^2 + (y - b)^2 = r^2`

In this case, the center of the circle is (-2, -3) and the radius is
`5 √(2)`

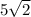
. So, the equation of the circle is:

`(x + 2)^2 + (y + 3)^2 = (5\sqrt2))^2`

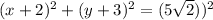
Expanding the squares and simplifying, we get the equation of the circle in standard form:

`x^2 + 4x + y^2 + 6y - 31 = 0`