Question

Prove the trigonometric identity
(tan x + cot x)/(csc x * cos x) = sec^2 x​

Answer 1

The proof of the trigonometric identity:

We can start by expanding the numerator and denominator. In the numerator, we can use the trigonometric identities tan x = sin x / cos x and cot x = cos x / sin x.

In the denominator, we can use the trigonometric identity csc x = 1 / sin x. This gives us:

`((tan x + cot x))/((csc x * cos x) ) = (((sin x )/( cos x)) + ((cos x )/(sin x)))/(((1)/( sin x)) * cos x)`

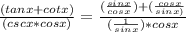
`We can then cancel the sin x terms in the numerator and denominator. This gives us:

`((tan x + cot x))/((csc x * cos x) ) = (1 + 1)/(((1 )/(sin x)) * cos x)`

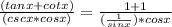
We can then multiply the numerator and denominator by sin x. This gives us:

`((tan x + cot x))/((csc x * cos x) ) = (sin x + sin x)/((1 )/(cos x))`

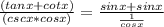
We can then simplify the expression. This gives us:

`((tan x + cot x))/((csc x * cos x) ) = (2sin x)/((1 )/(cos x)) = (2sin x)/(cos x) = 2tan x`

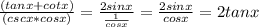
Finally, we can use the trigonometric identity tan^2 x = sec^2 x - 1 to get:

`2tan x =( 2tan^2 x )/( (sec^2 x - 1))`

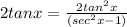
This gives us the following identity:

`((tan x + cot x))/((csc x * cos x) ) = sec^2 x`

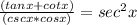
This completes the proof of the trigonometric identity.

Answer 2

`(\tan x + \cot x)/(\csc x \cos x)=\sec^2 x`

`\boxed{((\sin x)/(\cos x) + (\cos x)/(\sin x))/((1)/(\sin x) \cdot \cos x)}=\sec^2 x`

`\boxed{((\sin^2 x)/(\sin x\cos x) + (\cos^2 x)/(\sin x \cos x))/((\cos x)/(\sin x))}=\sec^2 x`

`\boxed{((\sin^2 x+\cos^2 x)/(\sin x\cos x))/((\cos x)/(\sin x))}=\sec^2 x`

`\boxed{((1)/(\sin x\cos x))/((\cos x)/(\sin x))}=\sec^2 x`

`\boxed{(1)/(\sin x\cos x) \cdot (\sin x)/(\cos x)}=\sec^2 x`

`(1)/(\cos^2x)=\sec^2x`

`\sec^2x=\sec^2x`

Explanation:

Given trigonometric identity:

`(\tan x + \cot x)/(\csc x \cos x)=\sec^2 x`

`\textsf{Use the identities\;\;$\tan x = (\sin x)/(\cos x)$\;,\;$\cot x=(\cos x)/(\sin x)$\;\;and\;\;$\csc x=(1)/(\sin x)$}:`

`\boxed{((\sin x)/(\cos x) + (\cos x)/(\sin x))/((1)/(\sin x) \cdot \cos x)}=\sec^2 x`

Simplify the denominator and make the fractions in the numerator like fractions:

`\boxed{((\sin^2 x)/(\sin x\cos x) + (\cos^2 x)/(\sin x \cos x))/((\cos x)/(\sin x))}=\sec^2 x`

`\textsf{Apply\;the\;fraction\;rule\;\;$(a)/(b)+(c)/(b)=(a+c)/(b)$\;to\;the\;numerator}:`

`\boxed{((\sin^2 x+\cos^2 x)/(\sin x\cos x))/((\cos x)/(\sin x))}=\sec^2 x`

`\textsf{Use\;the\;identity\;\;$\sin^2x+\cos^2x=1$}:`

`\boxed{((1)/(\sin x\cos x))/((\cos x)/(\sin x))}=\sec^2 x`

`\textsf{Apply\;the\;fraction\;rule\;\;$(a)/((b)/(c))=a \cdot (c)/(b)$}:`

`\boxed{(1)/(\sin x\cos x) \cdot (\sin x)/(\cos x)}=\sec^2 x`

Cancel the common factor sin x, and apply the exponent rule aa = a² to the denominator:

`(1)/(\cos^2x)=\sec^2x`

`\textsf{Use the identity\;\;$(1)/(\cos x)=\sec x$}:`

`\sec^2x=\sec^2x`