Question

An animal researcher randomly selected 98 dogs and cats and recorded if they napped between 2:00 p. M. And 2:30 p. M. The two-way table displays the data.

A 4-column table with 3 rows. Column 1 has entries dog, cat, total. Column 2 is labeled nap with entries 15, 23, 38. Column 3 is labeled no nap with entries 32, 28, 60. Column 4 is labeled total with entries 47, 51, 98. The columns are titled napping habit and the rows are titled animal type.



Suppose an animal is randomly selected. Let event C = cat and let event N = nap. What is the value of P(C|N)?



StartFraction 38 Over 98 EndFraction


StartFraction 23 Over 51 EndFraction


StartFraction 47 Over 98 EndFraction


StartFraction 23 Over 38 EndFraction

Answer 1

The value of P(C|N), the probability that a randomly selected napping animal is a cat, is calculated using the formula P(C|N) = P(C ∩ N) / P(N). The correct value is 23 napping cats divided by the total 38 napping animals, resulting in a probability of 23/38.

Step-by-step explanation:

The question is asking us to calculate the conditional probability of a randomly selected animal being a cat, given that it does nap between 2:00 p.m. and 2:30 p.m. This conditional probability is denoted as P(C|N), where C is the event that an animal is a cat, and N is the event that the animal naps. To find this, we use the formula for conditional probability, P(C|N) = P(C ∩ N) / P(N), where P(C ∩ N) is the probability that the animal is both a cat and naps, and P(N) is the probability that the animal naps regardless of being a cat or dog.

From the two-way table, there are 23 cats that nap and there are a total of 38 animals that nap. The probability that a randomly selected napping animal is a cat is therefore the number of napping cats divided by the total number of napping animals, which is 23/38. None of the other options correctly represent this probability.

Answer 2

The value of ( P(C|N) ), the probability of selecting a cat given that the animal napped, is
`\( (23)/(38) \).`

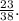
Step-by-step explanation:

The conditional probability ( P(C|N) ) represents the probability of an event occurring given that another event has already occurred. In this case, it is the probability of selecting a cat (C) given that the animal napped (N). To calculate this, we use the formula:

`\[ P(C|N) = (P(C \cap N))/(P(N)) \]`

where
`\(P(C \cap N)\)` is the probability of both events happening, and (P(N)) is the probability of the given event (nap) occurring.

From the table,
`\(P(C \cap N)\)` is the number of cats that napped, which is 23, and (P(N)) is the total number of animals that napped, which is 38. Therefore,

`\[ P(C|N) = (23)/(38) \]`

So, the correct answer is
`\( (23)/(38) \)`. This indicates that, given an animal napped between 2:00 p.m. and 2:30 p.m., there is a
`\( (23)/(38) \)` probability that it is a cat.

In summary, the probability ( P(C|N) ) is calculated by dividing the number of cats that napped by the total number of animals that napped. This ratio gives the likelihood of a randomly selected napping animal being a cat.