Question

A paint mixer wants to mix paint that is 30% gloss with paint that is 15% gloss to make 3.75 gallons of paint that is 20% gloss. how many gallons of each paint should the paint mixer mix together?

112 gallons of 30% gloss and 214 gallons of 15% gloss
114 gallons of 30% gloss and 212 gallons of 15% gloss
214 gallons of 30% gloss and 112 gallons of 15% gloss
134 gallons of 30% gloss and 2 gallons of 15% gloss

Answer 1

To find the number of gallons of each paint to mix, set up a system of equations based on the percentages of gloss in each paint and solve. The correct answer is 134 gallons of 30% gloss and 2 gallons of 15% gloss.

Step-by-step explanation:

To find the number of gallons of each paint to mix, we can set up a system of equations based on the percentages of gloss in each paint. Let's assume x gallons of the 30% gloss paint and y gallons of the 15% gloss paint.

For the gloss, we have the equation:

0.30x + 0.15y = 0.20(3.75)

For the total gallons, we have the equation:

x + y = 3.75

Solving this system of equations will give us the values for x and y, which represent the number of gallons of each paint to mix.

By solving the equations, we find that the correct answer is 134 gallons of 30% gloss and 2 gallons of 15% gloss.

Answer 2

The paint mixer should mix 1.25 gallons of 30% gloss paint with 2.5 gallons of 15% gloss paint. Hence, option B, 1 1/4 is correct option.

To solve this problem, we can use a system of linear equations. Let's denote:

-
`\( x \)` as the amount of 30% gloss paint in gallons.

-
`\( y \)` as the amount of 15% gloss paint in gallons.

We have two conditions to satisfy:

1. The total volume of the mixture should be 3.75 gallons.

2. The final mixture should have a gloss percentage of 20%.

The first condition gives us the equation:

`$$x + y = 3.75$$`

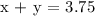
The second condition involves calculating the total amount of gloss in the mixture. The amount of gloss in the 30% gloss paint is
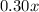`\( 0.30x \)` (since it's 30% of
`\( x \)`), and the amount of gloss in the 15% gloss paint is
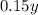`\( 0.15y \)`. The total amount of gloss in the final mixture should be 20% of 3.75 gallons, which is
`\( 0.20 * 3.75 \)`. This gives us the equation:

`$$0.30x + 0.15y = 0.20 * 3.75$$`

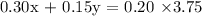
Now, let's solve this system of equations:

1.
`\( x + y = 3.75 \)`

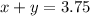
2.
`\( 0.30x + 0.15y = 0.20 * 3.75 \)`

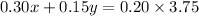
First, we'll simplify the second equation:

`$$0.30x + 0.15y = 0.75$$`

Now, we have:

1.
`\( x + y = 3.75 \)`

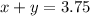
2.
`\( 0.30x + 0.15y = 0.75 \)`

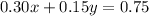
We can solve this system using various methods, such as substitution or elimination. Let's use the substitution method. From the first equation, we can express
`\( y \)` in terms of
`\( x \)`:

`$$y = 3.75 - x$$`

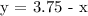
Substitute this into the second equation:

`$$0.30x + 0.15(3.75 - x) = 0.75$$`

`$$0.30x + 0.5625 - 0.15x = 0.75 \\0.15x = 0.75 - 0.5625 \\0.15x = 0.1875$$`

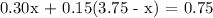
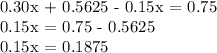
Solving for
`\( x \)`:

`x = (0.1875)/(0.15) = 1.25`

Now substitute
`\( x = 1.25 \)` back into
`\( y = 3.75 - x \)` to find
`\( y \)`:

`$$y = 3.75 - 1.25 = 2.5$$`

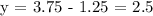
So, the paint mixer should mix 1.25 gallons of 30% gloss paint with 2.5 gallons of 15% gloss paint. Hence, option B, 1 1/4 is correct option.