Question

At a cell phone assembly plant, 79% of the cell phone keypads pass inspection. A random sample of 103 keypads is analyzed. Find the probability that more than 83% of the sample keypads pass inspection

Answer 1

The question asks for the probability of having more than 83% of cell phone keypads passing inspection from a sample of 103 when 79% usually pass. To solve this, one can either use the binomial distribution or a normal approximation depending on the sample size. Important values would include the number of keypads that represent 83% of the sample, the binomial probabilities, or the z-score associated with 83% in the normal distribution.

Step-by-step explanation:

The question involves finding the probability that more than 83% of the sample of 103 cell phone keypads pass inspection, given that 79% of the keypads pass inspection in general. This is a problem that can be solved using the concept of a binomial or a normal approximation to the binomial distribution since we are dealing with a percentage of a sample.

First, we calculate the number of keypads that represent 83% of the sample of 103, which is 0.83 * 103 = 85.49. Since the number of keypads must be whole, we round up to 86.

Then, if we want to use the binomial distribution directly, we could calculate the probability of exactly 86, 87, ..., 103 keypads passing inspection and then sum these probabilities. However, when the sample size is large, it's often easier to use a normal approximation to the binomial distribution.

With a normal approximation, we would calculate the mean and standard deviation for the distribution of sample proportions and then use these to calculate the z-score for 0.83. That z-score can then be used to find the probability in a standard normal distribution table or using a calculator equipped with statistics functions. However, detailed calculations are not provided here since these would require a more in-depth analysis and explanation.

Answer 2

there is approximately a 15.9% probability that more than 83% of the sample keypads will pass inspection.

To find the probability that more than 83% of the sample keypads pass inspection, we can use the normal approximation to the binomial distribution because the sample size is large enough. In this context, the binomial distribution parameters would be
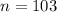`\( n = 103 \)` (the sample size) and
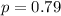`\( p = 0.79 \)` (the probability of success, which is a keypad passing inspection).

When approximating the binomial distribution with a normal distribution, we need to find the mean
`(\( \mu \))` and standard deviation (\( \sigma \)) of the binomial distribution which are given by:

`\[ \mu = n * p \]`

`\[ \sigma = √(n * p * (1 - p)) \]`

To find the probability that more than 83% of the sample keypads pass inspection, we need to:

1. Calculate the mean and standard deviation of the binomial distribution using the formulas above.

2. Convert the 83% to an actual number of keypads that would need to pass inspection to exceed this percentage.

3. Use the normal approximation to calculate the z-score for the number that represents more than 83% passing.

4. Use the standard normal distribution to find the probability that corresponds to this z-score.

Let's do these calculations.

Here are the step-wise calculations:

1. The mean
`(\( \mu \))` of the binomial distribution is calculated as:

`\[ \mu = n * p = 103 * 0.79 = 81.37 \]`

2. The standard deviation (\( \sigma \)) of the binomial distribution is:

`\[ \sigma = √(n * p * (1 - p)) = √(103 * 0.79 * (1 - 0.79)) \approx 4.13 \]`

3. To find the corresponding number of keypads for 83%, we calculate:

`\[ \text{Number of keypads passing} = \lceil 103 * 0.83 \rceil = 86 \]`

(We use the ceiling function to round up since we cannot have a fraction of a keypad.)

4. The z-score is calculated for the continuity corrected value (86 - 0.5 keypads) as follows:

`\[ z = (85.5 - \mu)/(\sigma) \approx (85.5 - 81.37)/(4.13) \approx 1.00 \]`

5. The probability of more than 83% of the keypads passing inspection is the area to the right of this z-score in the standard normal distribution:

`\[ P(Z > 1.00) \approx 0.159 \]`

So, there is approximately a 15.9% probability that more than 83% of the sample keypads will pass inspection.