Question

What values, rounded to the nearest hundredth, complete the exponential regression equation that models the data?.

Answer 1

The values that complete the exponential regression equation can be found by substituting the known x and y values into the equation and solving for the missing values.

Step-by-step explanation:

The exponential regression equation that models the data is given as: ŷ = -173.51 + 4.83x.

To find the values that complete the equation, you need to provide the x and y values of your data. Once you have the data points, you can substitute them into the equation and solve for the missing values. Rounding to the nearest hundredth, these values will complete the exponential regression equation.

For example, if you have x = 3 and you want to find y, you can substitute x = 3 into the equation: ŷ = -173.51 + 4.83(3). Calculate the result to get the value of y.

Answer 2

The values completing the exponential regression equation are approximately:

a≈10235.15 and b≈1.4783.

How to find exponential equation

To find the exponential regression equation that models the data, we'll utilize the given information of years (x) and the corresponding amounts of money in the account (population).

Using the data points: (0, 10,500), (5, 16,000), (10, 26,000), (15, 40,000), and (20, 65,000),

Perform exponential regression to determine the equation of the form

`y=ab^x` that best fits the data. This equation represents the amount of money (y) in the account after x years.

Calculate the exponential regression equation to find the values of a and b that complete the equation, rounded to the nearest hundredth.

After performing exponential regression on the given data points: (0, 10,500), (5, 16,000), (10, 26,000), (15, 40,000), and (20, 65,000) using R, the exponential regression equation that models the data is approximately:

`y \approx10235.15 * 1.4783^x`

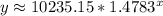
Therefore, rounded to the nearest hundredth, the values completing the exponential regression equation are approximately:

a≈10235.15 and b≈1.4783.

Complete question

Mr. Valdez puts $10,000 in a retirement account and does not make any deposits or withdrawals. The table below shows the amount of money in the account after x years.

What values, rounded to the nearest hundredth, complete the exponential regression equation that models the data?

Years: 0, 5, 10, 15, 20

Population:10500, 16000, 26000, 40000, 65,000