Question

Work out an approximate solution to x3 + 2x – 1 = 0

Use the iteration Xn+ 1 =


1


x + 2


Start with Xy = 1


Give your answer to 2 decimal places.

Answer 1

x = 0.45 (2 d.p.)

Explanation:

Iteration is a numerical method used to approximate solutions to equations where exact solutions are difficult or impossible to obtain analytically.

It involves putting an approximate value of the solution into an iteration formula to calculate a new value based on the previous one. This process is repeated multiple times, with each iteration generating a more accurate approximation of the solution.

The iteration formula is just a rearrangement of the equation, leaving a single ‘x’ on one side.

For this problem, we have already been given the iteration formula and the starting value of x₁. However, sometimes you will need to determine the iteration formula. For example, to determine the iteration formula for x³ + 2x - 1 = 0, rearrange the equation as follows:

`\begin{aligned}x^3+2x-1&=0\\x^3+2x&=1\\x(x^2+2)&=1\\x&=(1)/(x^2+2)\end{aligned}`

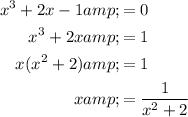
Therefore, the iteration formula is:

`\boxed{x_(n+1)=\frac{1}{{x_n}^2+2}}`

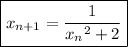
To calculate the approximate solution to x³ + 2x - 1 = 0 using the given iteration formula, start by substituting x₁ = 1 into the formula to find x₂:

`x_2=\frac{1}{x_(1){^2}+2}=(1)/((1)^2+2)=(1)/(1+2)=(1)/(3)=0.3333...`

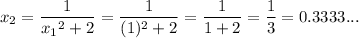
Substitute the found value of x₂ into the formula to find the value of x₃:

`x_3=\frac{1}{x_(2){^2}+2}=(1)/(\left((1)/(3)\right)^2+2)=(1)/((1)/(9)+2)=(1)/((19)/(9))=(9)/(19)=0.47368...`

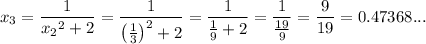
Continue this way until the solutions are the same when rounded to 2 d.p:

`x_4=0.44956...`

`x_5=0.45411...`

`x_6=0.45326...`

`x_7=0.45342...`

`x_8=0.45339...`

`x_9=0.45339...`

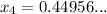
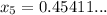
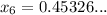
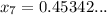
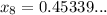
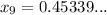
Therefore, the approximate solution to x³ + 2x - 1 = 0 is 0.45, rounded to 2 decimal places.

Additional information

The quickest way to compute each solution (each value in the iteration sequence) is to enter the value of x₁ into the calculator and press "=" so that the value of x₁ becomes the "answer". Then type the iteration formula into the calculator, replacing xₙ with "answer":

`\boxed{\frac{1}{\text{Ans}^2+2}}`

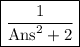
Each time you press "=", the next value of xₙ in the sequence is computed.