Answer:
1) False
2) True
3) False
Explanation:
From inspection of the attached unit circle, we can see that:
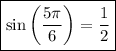
Therefore, the first statement is false.

The tangent function is periodic with a period of π, meaning that for any integer n:
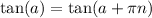
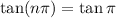
Therefore:
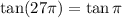
From the unit circle we can see that:

Therefore,

Therefore, the second statement is true.


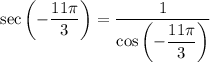
The cosine function is periodic with a period of 2π, meaning that for any integer n:
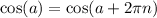
Therefore:

From the unit circle we can see that:
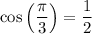
Therefore:
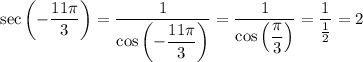
Therefore, the third statement is false.