Question

For the function , continuity

Answer 1

Answer: Choice C

Condition 1 fails.
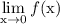`\displaystyle \lim_{\text{x} \to 0}f(\text{x})` does not exist

====================================

Step-by-step explanation:

Use a table or a graph to determine that
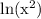`\ln(\text{x}^2)` approaches negative infinity as x gets closer to 0.

Symbolically
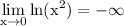`\displaystyle \lim_{\text{x} \to 0}\ln(\text{x}^2) = -\infty`. Since this result is not a finite number, we consider the limit to not exist. Write "DNE" as shorthand for "does not exist".

Therefore,
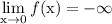`\displaystyle \lim_{\text{x} \to 0}f(\text{x}) = -\infty` making
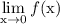`\displaystyle \lim_{\text{x} \to 0}f(\text{x})` not exist as well.