Question

For the function
please help

Answer 1

Answer: B

Step-by-step explanation:

In order to find out if the functions are continuous at 0, you must plug in 0 into both of the piecewise equations. If the answers are the same then they are continuous at 0 if they are different then it is not continuous.

e× + 1

e⁰ + 1

1 +1

2

2 + sin x

2 + sin 0

2 + 0

2

Since the first part equation =2 when x=0 and the second part equation =0 when x=0, the functions would be continuous because they are the same. But because there is no ≤ or ≥ there is no value for x=0. It's been removed.

Your answer is B

Answer 2

Answer: Choice B

The function f is continuous on
`(-\infty,0) \cup (0,\infty)`

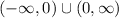
There is a removable discontinuity at x = 0.

====================================================

Step-by-step explanation:

Let

`g(\text{x}) = e^{\text{x}}+1\\h(\text{x}) = 2+\sin({\text{x}})\\`

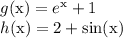
The f(x) function changes its identity based on what the input x would be.

If x < 0, then f(x) = g(x)

If x > 0, then f(x) = h(x)

Plug x = 0 into g(x)

`g(\text{x}) = e^{\text{x}}+1\\g(0) = e^(0)+1\\g(0) = 1+1\\g(0) = 2\\`

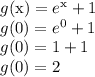
Do the same for h(x)

`h(\text{x}) = 2+\sin({\text{x}})\\h(0) = 2+\sin(0)\\h(0) = 2+0\\h(0) = 2\\`

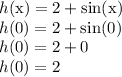
Both functions produce the same output (2) when x = 0. Therefore, the two pieces are connected. Both pieces approach y = 2 when x gets closer and closer to zero. But we'll have an open hole at x = 0 since neither piece is defined when x = 0. This makes f(0) undefined. We have a removable discontinuity at x = 0. This is in contrast to a jump discontinuity where the two pieces do not approach the same y value.

To express this in interval notation, start with the set of real numbers
`(-\infty,\infty)` and poke a hole at x = 0 to remove it.

We'll end up with
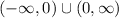`(-\infty,0) \cup (0,\infty)` as the domain and where f(x) is continuous.

Refer to the graph below.