Question

Drag each tile to the correct box. Arrange the angles in increasing order of their cosines.

3(pi)/4
(pi)
7(pi)/6
5(pi)/3
7(pi)/4
4(pi)/3
3(pi)/2
2(pi)

Answer 1

The cosine values of the angles are arranged in the following manner in increasing order:-(5π)/3,-(7π)/6,-(3π)/4,-π/2,-π/3,-π/4,0,1. The cosine is obtained by dividing the adjacent side by the hypotenuse of the right triangle that is formed from the angle, using the cosine formula.

Cos(θ) = Adjacent side / Hypotenuse.

Step-by-step explanation:

Given a set of angles in increasing order of their cosines are as follows:-

3(pi)/4(pi)7(pi)/65(pi)/37(pi)/44(pi)/33(pi)/22(pi)

We know the cosine of an angle measures the ratio of the adjacent side to the hypotenuse of a right-angled triangle in which the angle is being referred to. So, we need to find the cosine of all the given angles.

`Cos ((3\pi )/(4))`

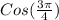
= -(√2)/2Cos (π)

= -1Cos (7π/6)

= -√3/2Cos (5π/3)

= 1/2Cos (7π/4)

= (√2)/2Cos (4π/3)

= -1/2Cos (3π/2)

= 0Cos (2π)

= 1

Arrange the cosine values in increasing order: (5π)/3,-(7π)/6,-(3π)/4,-π/2,-π/3,-π/4,0,1.