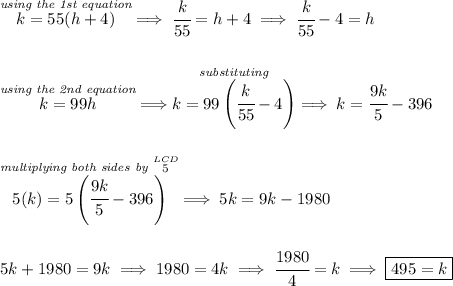Question

The trains will meet ___ km
Thank u for help :-)

Answer 1

k = kilometers travelled when the trains meet.

Well, the 1st takes off at 55 km/h and 4 hour later the Express one takes off, well if the Express by the times it catches up with the 1st one has travelled "h" hours, then the 1st train since it left 4 hours earlier, has been going on for "h + 4" hours.

Now, when both meet well, heck, the distance "k" kilometers is the same for both, otherwise they wouldn't be meeting.

`{\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{km s}{distance}&\stackrel{k ph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ \textit{Earlier Train}&k&55&h+4\\ \textit{Express Train}&k&99&h \end{array}\hspace{5em} \begin{cases} k=(55)(h+4)\\\\ k=(99)(h) \end{cases} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{using the 1st equation}}{k=55(h+4)}\implies \cfrac{k}{55}=h+4\implies \cfrac{k}{55}-4=h \\\\\\ \stackrel{\textit{using the 2nd equation}}{k=99h}\implies \stackrel{\textit{substituting}}{k=99\left( \cfrac{k}{55}-4 \right)}\implies k=\cfrac{9k}{5}-396 \\\\\\ \stackrel{\textit{multiplying both sides by }\stackrel{LCD}{5}}{5(k)=5\left( \cfrac{9k}{5}-396 \right)}\implies 5k=9k-1980 \\\\\\ 5k+1980=9k\implies 1980=4k\implies \cfrac{1980}{4}=k\implies \boxed{495=k}`