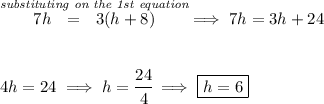Question

Help urgent thank you for help :-)

Answer 1

h = hours taken by Mini to catch up with Willie

Now, by the time Mini catches up with Willie, we can say that by then Mini has travelled "m" miles and Willie has travelled, well, she caught up with him, so hell he travelled the same "m" miles too.

If Mini took "h" hours travelling and Willie had left 8 hours earlier, that means that Willie has travelled 8 hours plus whatever Mini travelled, or "h", so Willie has travelled "h + 8" hours by the time they met.

`{\Large \begin{array}{llll} \underset{distance}{d}=\underset{rate}{r} \stackrel{time}{t} \end{array}} \\\\[-0.35em] ~\dotfill\\\\ \begin{array}{lcccl} &\stackrel{miles}{distance}&\stackrel{mph}{rate}&\stackrel{hours}{time}\\ \cline{2-4}&\\ Willie&m&3&h+8\\ Mini&m&7&h \end{array}\hspace{5em} \begin{cases} m=(3)(h+8)\\\\ m=(7)(h) \end{cases} \\\\[-0.35em] ~\dotfill`

`\stackrel{\textit{substituting on the 1st equation}}{7h~~ = ~~3(h+8)}\implies 7h=3h+24 \\\\\\ 4h=24\implies h=\cfrac{24}{4}\implies \boxed{h=6}`