Question

Which value of x makes this inequality true? x+9<4x

A.4
B.1
C.3
D.2

Answer 1

A. 4

Explanation:

Given inequality:

`x+9 < 4x`

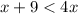
Rearrange the inequality to isolate x.

Subtract x from both sides of the inequality:

`\begin{aligned}x+9-x & < 4x-x\\9& < 3x\end{aligned}`

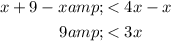
Divide both sides of the inequality by 3:

`\begin{aligned}(9)/(3)& < (3x)/(3)\\\\3& < x\\\\x& > 3\end{aligned}`

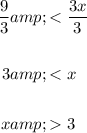
So the values of x that make the inequality true are:

• Any value of x that is greater than 3.

Therefore, from the given answer options, the value of x that makes the inequality true is x = 4.

To check this, substitute x = 4 into the inequality:

`\begin{aligned}x+9& < 4x\\x=4\implies 4+9& < 4(4)\\13& < 16\end{aligned}`

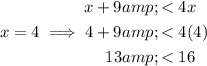
As 13 is less than 16, the inequality is true when x = 4.