Question

Write an equation in slope-intercept form of the line satisfying the following conditions. through (6,9); perpendicular to x = 8

Answer 1

y = 9

Explanation:

it's perpendicular to x = 8 which is a vertical line, so our line will be horizontal line with slope 0 and it goes through (6,9) so at x = 6, y =9

but since the line is horizontal, (slope = 0) it must have the same y-value at all x- points so,

the equation is y = 9

Answer 2

The equation is :

↬ y = 9

Solution:

If two lines are perpendicular, their slopes are opposite reciprocals of each other.

Since we have a vertical line, its slope is undefined. Now, remember the definition of perpendicular lines. They intersect at a right angle.

And the line that is perpendicular to a vertical line is a horizontal line, which has a slope of 0.

Lines with 0 slope have the appearance of y = b where b is the y intercept.

Now there are two ways to find the y-intercept, which are :

• Using point slope and simplifying all the way to slope intercept
• Plugging in (6, 9) into
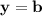  `\bf{y=b}` and solving for b.

Allow me to demonstrate the first one.

Method 1. Point slope

Point slope is
`\bf{y-y_1=m(x-x_1)}`.

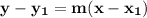Plugging in the numbers
`\bf{y-9=0(x-6)}`

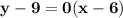
Simplifying
`\bf{y-9=0}`

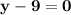
Simplifying further

`\bf{y=9}`

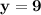
Hence, the equation is
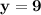`\bf{y=9}`.