Question

If R denotes the reaction of the body to some stimulus of strength x, the sensitivity S is defined to be the rate of change of the reaction with respect to x. A particular example is that when the brightness x of a light source is increased, the eye reacts by decreasing the area R of the pupil. The experimental formula R=[(40+24x^4)/(1+4x^4)] has been used to model the dependence of R on x when R is measured in sq mm and x is measured in the appropriateunits of brightness.

Find the sensitivity.

R'(x)=

Answer 1

To find the sensitivity (rate of change of the reaction) to the brightness x of a light source, we need to find the derivative of the experimental formula R=(40+24x^4)/(1+4x^4) concerning x. Using the quotient rule to find the derivative, we get R'(x) = -544x^3 / (1+4x^4)^2.

Step-by-step explanation:

The sensitivity of a sensory system to a stimulus is defined as the rate of change of the reaction to the stimulus. In this case, the stimulus is the brightness of a light source (x) and the reaction is the decrease in the area of the pupil (R). The experimental formula for the relationship between R and x is given as R=(40+24x^4)/(1+4x^4). To find the sensitivity, we need to find the derivative of R concerning x, which is denoted as R'(x).

Using the quotient rule, we can find the derivative:

R'(x) = [
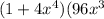`(1+4x^4)(96x^3`(16x^3)] / (1+4x^4)^2

Simplifying further, we get:

R'(x) = [96x^3 + 384x^7 - 640x^3 - 384x^7] / (1+4x^4)^2

R'(x) = -544x^3 / (1+4x^4)^2