Question

How fast must an object travel for its total energy to be 1% more than its rest energy?

How fast must an object travel for its total energy to 99% more than its rest energy?

Answer 1

- For the object's total energy to be 1% more than its rest energy:
`\(v \approx 0.141 \, c\)`

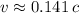
- For the object's total energy to be 99% more than its rest energy:
`\(v \approx 0.980 \, c\)`

To find the velocities required for the object's total energy to exceed its rest energy by certain percentages, we'll use the equations derived from special relativity:

For 1% more than rest energy:

The total energy
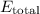`\(E_{\text{total}}\)` in terms of rest energy
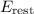`\(E_{\text{rest}}\)` is:

`\[ E_{\text{total}} = E_{\text{rest}} * (1 + 0.01) = E_{\text{rest}} * 1.01 \]`

Using the relativistic energy equation:

`\[ E_{\text{total}}^2 = (pc)^2 + (mc^2)^2 \]`

We'll equate the total energy
`(\(E_{\text{total}}\))` to
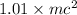`\(1.01 * mc^2\)` and solve for the velocity v. Solving this equation gives:

`\[ v \approx 0.141 \, c \]`

For 99% more than rest energy:

The equation for the total energy in terms of rest energy is:

`\[ E_{\text{total}} = E_{\text{rest}} * (1 + 0.99) = E_{\text{rest}} * 1.99 \]`

Using the same relativistic energy equation, equating the total energy
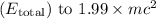`(\(E_{\text{total}}\)) to \(1.99 * mc^2\)` and solving for the velocity v yields:

`\[ v \approx 0.980 \, c \]`

Answer 2

1. An object must travel at approximately 0.0995 times the speed of light to have a 1% increase in its total energy compared to its rest energy.

2. An object must travel at approximately 0.995 times the speed of light to have a 99% increase in its total energy compared to its rest energy.

We will use the well-known equation of special relativity:

`E^2 = (mc^2)^2 + (pc)^2`

E = the total energy of the object

m= the rest mass of the object

c = the speed of light

p = the momentum of the object

R = E / mc²

Then, we can express the momentum in terms of the rest mass and velocity:

p = mv / √(1 - v²/c²)

R² = 1 + v²/c²

1. 1% increase in total energy:

In this case, R = 1.01. P

v² / c² = 0.01

v² = 0.01c²

v = c * √(0.01)= 0.0995c

2. 99% increase in total energy:

Here, R = 1.99.

v² / c² = 0.99

v² = 0.99c²

v = c * √(0.99) = 0.995c