Question

I am confused on finding the answer i have tried a few times and i do not understand

Answer 1

11.9 cubic inches

Explanation:

The explanation is attached below.

Answer 2

11.9 in³

Explanation:

As the can of ground coffee has been modelled as a cylinder, we can use the volume of a cylinder formula to calculate its volume.

`\boxed{\begin{minipage}{4 cm}\underline{Volume of a cylinder}\\\\$V=\pi r^2 h$\\\\where:\\ \phantom{ww}$\bullet$ $r$ is the radius. \\ \phantom{ww}$\bullet$ $h$ is the height.\\\end{minipage}}`

We are told that:

`\bullet \quad \textsf{Height, $h$}=6(3)/(4)\; \sf inches`

`\bullet \quad \textsf{Radius, $r$}=(3)/(4)\; \sf inches`

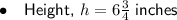
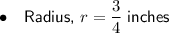
First, convert the mixed fraction of the height into an improper fraction:

`\textsf{Height, $h$}=6 (3)/(4)=(6 \cdot 4+3)/(4)=(24+3)/(4)=(27)/(4)`

Now, substitute the values of h and r into the formula for volume:

`V=\pi \cdot \left((3)/(4)\right)^2 \cdot \left( (27)/(4)\right)`

`\textsf{Apply the exponent rule:} \quad \left((a)/(b)\right)^c=(a^c)/(b^c)`

`V=\pi \cdot \left((3^2)/(4^2)\right) \cdot \left( (27)/(4)\right)`

`V=\pi \cdot \left((9)/(16)\right) \cdot \left( (27)/(4)\right)`

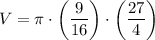
Multiply the fractions by multiplying the numerators and the denominators:

`V=\pi \cdot \left((9 \cdot 27)/(16 \cdot 4)\right)`

`V=\pi \cdot \left((243)/(64)\right)`

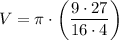
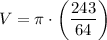
Now we have calculated the volume in terms of π.

Use a calculator to multiply the improper fraction by π:

`V=\pi \cdot \left((243)/(64)\right)=11.9282346...`

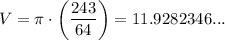
Rounding this to the nearest tenth gives:

`\boxed{V = 11.9\; \sf in^3}`

Therefore, the volume of the coffee can is 11.9 in³ to the nearest tenth.

Note: If you use π = 3.14 or π = 22/7, the final answer is still 11.9 in³.