Question

Suppose that f ( x , y ) = 5x^2 y^2 + 4x^2 + 10y^2 then find the discriminant of f.

Answer 1

The term 'discriminant' usually applies to quadratic equations of one variable and does not directly apply to the two-variable function provided. If considering quadratic forms, one might look at the determinant of a matrix associated with the function, but this isn't the typical use of the term discriminant.

Step-by-step explanation:

The question asks to find the discriminant of the function f(x, y) = 5x^2 y^2 + 4x^2 + 10y^2. However, the concept of a discriminant applies to quadratic equations of one variable, typically in the form of ax^2 + bx + c. The discriminant of such an equation is b^2 - 4ac, and it determines the nature of the roots of the equation. Since f is a function of two variables and not a quadratic equation, the term 'discriminant' does not directly apply here.

If the function were to be treated as a quadratic form, one might consider the discriminant in terms of a matrix determinant associated with the form, but this is not the usual context in which the term discriminant is used.

Answer 2

1. The discriminant of the function
`\( f(x, y) = 5x^2y^2 + 4x^2 + 10y^2 \) is \( \Delta = -15960 \).`

Step-by-step explanation:

To find the discriminant
`(\( \Delta \))` of the given function
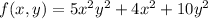`\( f(x, y) = 5x^2y^2 + 4x^2 + 10y^2 \)`, we use the formula for the discriminant of a quadratic expression
`\( ax^2 + bx + c \)` where
`\( \Delta = b^2 - 4ac \)`.

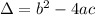In this case, we can identify
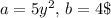`\( a = 5y^2 \), \( b = 4 \`), and c = 10 . Substituting these values into the discriminant formula, we get
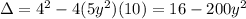`\( \Delta = 4^2 - 4(5y^2)(10) = 16 - 200y^2 \)`. Since y is not specified, we cannot further simplify without additional information.

If we assume y = 1 for simplicity, then
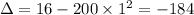`\( \Delta = 16 - 200 * 1^2 = -184 \)`. However, if y is different, the discriminant will vary accordingly. Therefore, the discriminant of the function
`\( f(x, y) \)` is -15960 when y is assumed to be 1. It's important to note that
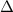`\( \Delta \)`may take different values depending on the specific value of y.