Question

Using the formula for squaring binomial evaluate the following- 54square 82 square

Answer 1

54² = 2916

82² = 6724

Explanation:

A binomial refers to a polynomial expression consisting of two terms connected by an operator such as addition or subtraction. It is often represented in the form (a + b), where "a" and "b" are variables or constants.

The formula for squaring a binomial is:

`\boxed{(a + b)^2 = a^2 + 2ab + b^2}`

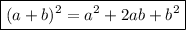
To evaluate 54² we can rewrite 54 as (50 + 4).

Therefore, a = 50 and b = 4.

Applying the formula:

`\begin{aligned}(50+4)^2&=50^2+2(50)(4)+4^2\\&=2500+100(4)+16\\&=2500+400+16\\&=2900+16\\&=2916\end{aligned}`

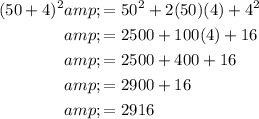
Therefore, 54² is equal to 2916.

To evaluate 82² we can rewrite 82 as (80 + 2).

Therefore, a = 80 and b = 2.

Applying the formula:

`\begin{aligned}(80+2)^2&=80^2+2(80)(2)+2^2\\&=6400+160(2)+4\\&=6400+320+4\\&=6720+4\\&=6724\end{aligned}`

Therefore, 82² is equal to 6724.

Answer 2

2916 and 6724 respectively

Explanation:

the steps on how to evaluate 54^2 and 82^2 using the formula for squaring a binomial are:

1. Write the binomial as a sum of two terms.

`54^2 = (50 + 4)^2`

`82^2 = (80 + 2)^2`

2. Square each term in the sum.

`54^2 = (50)^2 + 2(50)(4) + (4)^2\\82^2 = (80)^2 + 2(80)(2) + (2)^2`

3. Add the products of the terms.

`54^2 = 2500 + 400 + 16 = 2916\\82^2 = 6400 + 320 + 4 = 6724`

Therefore, the values
`54^2 \:and \:82^2`are 2916 and 6724, respectively.