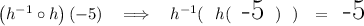let's keep in mind that an inverse function has the same x,y pairs as the original function but flipped sideways, another mouthful way to put it is, the domain of the original function is the range of the inverse and the range of the original is the domain of the inverse.
well, since that's the case for g(x), Check the picture below.
now let's check for h⁻¹(x)
as you already know, to get the inverse of any expression we start off by doing a quick switcheroo on the variables and then solving for "y", let's do so.
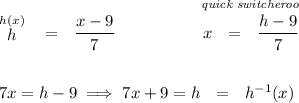
now, what's
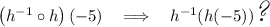
we know that h(x) is a one-to-one function and its inverse is a function, since that's the case h⁻¹( h(x) ) = x.
what the heck all that means? well, it simply means that