Answer:
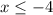
There will be a filled-in hole at -4.
Explanation:
We can solve an inequality the same way we do for equations. The only thing to keep in mind, is that multiplying by a negative number will result in flipping the inequality sign (< to > and vice versa)

The difference between a filled-in and an empty hole in terms of inequality graphs, is whether or not the number limiting the inequality is included in it.
For example, in x > 3, 3 is limiting the inequality, however, it is not included in it, therefore, x would always be greater than 3.
In another example,
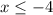 , -4 is limiting inequality and is included in it. Therefore, x would always be less than or equal to -4.
, -4 is limiting inequality and is included in it. Therefore, x would always be less than or equal to -4.
A filled-in hole means the number is included in the inequality, while an empty one means it isn't.
In our cases, -4 is included in the inequality (notice the line under the inequality sign that resembles "less than or equal to"), therefore there will be a filled-in hole at -4.