Question

The quadratic function f(x) has roots of −4 and 3 and point (2, −6) lies on f(x). What is the equation of f(x)? f(x) = (x + 3)(x − 4) f(x) = (x − 3)(x + 4) f(x) = 3(x + 3)(x − 4) f(x) = 3(x − 3)(x + 4)

Answer 1

`\displaystyle{f(x)=(x+4)(x-3)}`, the second choice.

Explanation:

Since the problem gives us that the quadratic function has roots of -4 and 3. Therefore, this means that:

`\displaystyle{x=-4,3}`

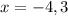
Which can be reverted back to:

`\displaystyle{f(x)=(x+4)(x-3)}`

However, we cannot assume that a = 1 in this case, so:

`\displaystyle{f(x)=a(x+4)(x-3)}`

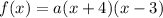
To clear any confusions, a means how narrow or wide the graph is, the same a-term in standard form or vertex form.

As the point (2, -6) is said to lie on f(x), therefore, substitute x = 2 and y = -6 to solve for a:

`\displaystyle{-6=a(2+4)(2-3)}\\\\\displaystyle{-6=a(6)(-1)}\\\\\displaystyle{-6=-6a}\\\\\displaystyle{a=1}`

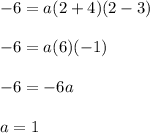
Therefore, a = 1. Thus, the equation of f(x) is:

`\displaystyle{f(x)=(x+4)(x-3)}`