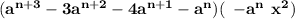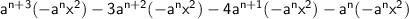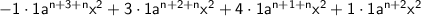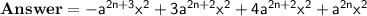Question :

Step by step explanation :
Case of multiplication of a Polynomial by a monomial. The rule says that, to multiply the monomial by each of the terms of the polynomial, taking into account the law of signs, separating the partial products with their own signs. That is, we apply the Distributive Law of multiplication.
Then, we will solve by Distributive law.