Question

NO LINKS!! URGENT HELP PLEASE!!

O is the center of the regular nonagon below. Find its area. Round to the nearest tenth if necessary.

Answer 1

471.1 square units

Explanation:

A regular nonagon is a 9-sided polygon with sides of equal length.

The apothem of a regular polygon is the distance from the center of the polygon to the midpoint of one of its sides.

Therefore, the given diagram shows a regular nonagon with an apothem of 12 units.

The side length (s) of a regular polygon can be calculated using the apothem formula:

`\boxed{\begin{minipage}{5.5cm}\underline{Apothem of a regular polygon}\\\\$a=(s)/(2 \tan\left((180^(\circ))/(n)\right))$\\\\where:\\\phantom{ww}$\bullet$ $s$ is the side length.\\ \phantom{ww}$\bullet$ $n$ is the number of sides.\\\end{minipage}}`

Given values:

• a = 12
• n = 9

Substitute the given values into the formula to create an expression for the side length (s):

`12=(s)/(2 \tan\left((180^(\circ))/(9)\right))`

`12=(s)/(2 \tan\left(20^(\circ)\right))`

`s=24 \tan\left(20^(\circ)\right)`

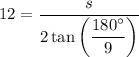
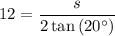
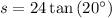
The standard formula for an area of a regular polygon is:

`\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=(n\cdot s\cdot a)/(2)$\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the length of one side.\\ \phantom{ww}$\bullet$ $a$ is the apothem.\\\end{minipage}}`

Substitute the found expression for s together with n = 9 and a = 12 into the formula and solve for A:

`A=(9 \cdot 24 \tan(20^(\circ)) \cdot 12)/(2)`

`A=1296\tan(20^(\circ))`

`A=471.705423...`

`A=471.7\; \sf square\;units\;(nearest\;tenth)`

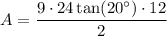
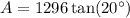
Therefore, the area of a regular nonagon with an apothem of 12 units is 471.1 square units, rounded to the nearest tenth.