Answer:
Approximately
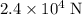 .
.
Step-by-step explanation:
Assume that the acceleration
 of the cannonball is constant while in the muzzle. Apply the following SUVAT equation to find this acceleration:
of the cannonball is constant while in the muzzle. Apply the following SUVAT equation to find this acceleration:
 .
.
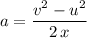 ,
,
Where:
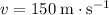 is the velocity after the acceleration,
is the velocity after the acceleration,
 is the initial velocity (assuming the cannonball was initially not moving,) and
is the initial velocity (assuming the cannonball was initially not moving,) and
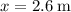 is the displacement during the acceleration.
is the displacement during the acceleration.
Thus, under the assumptions, acceleration of the cannonball in the muzzle would be:
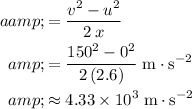 .
.
It is given that the mass of this cannonball is
 . By Newton's Laws of Motion, the net force on the cannonball would be:
. By Newton's Laws of Motion, the net force on the cannonball would be:
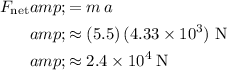 .
.