Question

The volume of the rectangular pyramid below is 468 units. Find the value of x.

Answer 1

12

Explanation:

Note that the area B of the rectangular base with length x and width 9 units is:

`B=9x`

Then, the volume
`V=468` cubic units of the pyramid is related to its base area
`B=9x` and height
`h=13` as follows:

`V=(1)/(3)Bh\\468=(1)/(3)* 9x* 13\\x=(468*3)/(9* 13)=12`

So, the value of x is 12.

Answer 2

Hello !

Answer:

`\Large \boxed{\sf x=12}`

Explanation:

The volume of a pyramid is given by
`\sf V_(pyramid)=(1)/(3)* B* h` where B is the area of the base and h is the height.

This is a rectangular pyramid. We have
`\sf B=l* w` where l is the length and w is the witdth.

So
`\sf V_(pyramid)=(1)/(3)* l * w* h`

Given :

• l = x
• w = 9
• h = 13

Let's substitute l, w and h with their values in the previous formula :

`\sf V_(pyramid)=(1)/(3)* x* 9 * 13\\\sf V_(pyramid)=3*13* x\\\sf V_(pyramid)=39x`

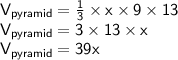
Moreover, we know that
`\sf V_(pyramid)=468\ units^3`.

Therefore
`\sf 39x=468`

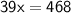
Let's solve for x :

Divide both sides by 39 :

`\sf (39x)/(39) =(468)/(39) \\\boxed{\sf x=12}`

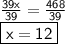
Have a nice day ;)