Question

NO LINKS!! URGENT HELP PLEASE!!

O is the center of the regular decagon below. Find its area. Round to the nearest tenth if necessary.

Answer 1

`\underset{ \textit{angle in degrees} }{\textit{area of a regular polygon}}\\\\ A=\cfrac{nr^2}{2}\sin((360)/(n)) ~~ \begin{cases} r=\stackrel{ circumcircle's }{radius}\\ n=sides\\[-0.5em] \hrulefill\\ n=10\\ r=13 \end{cases}\implies A=\cfrac{(10)(13)^2}{2}\sin((360)/(10)) \\\\\\ A=845\sin(36^o)\implies A\approx 496.7`

Answer 2

496.7 square units

Explanation:

A regular polygon is a polygon with equal side lengths and equal interior angles, meaning all of its sides and angles are congruent.

The radius of a regular polygon is the distance from the center of the polygon to any of its vertices.

The given figure is a regular decagon (10-sided figure) with a radius of 13 units.

To find the area of a regular polygon given its radius, use the following formula:

`\boxed{\begin{minipage}{6cm}\underline{Area of a regular polygon}\\\\$A=nr^2\sin \left((180^(\circ))/(n)\right)\cos\left((180^(\circ))/(n)\right)$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $r$ is the radius.\\\end{minipage}}`

Substitute n = 10 and r = 13 into the formula and solve for A:

`A=10 \cdot 13^2 \cdot \sin\left((180^(\circ))/(10)\right)\cdot \cos\left((180^(\circ))/(10)\right)`

`A=10 \cdot 169 \cdot \sin\left(18^(\circ)\right) \cdot \cos \left(18^(\circ)\right)`

`A=496.678538...`

`A=496.7\; \sf square \; units`

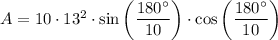
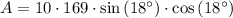
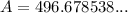
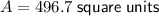
Therefore, the area of a regular decagon with a radius of 13 units is 496.7 square units (to the nearest tenth).